Estimating Square Roots Worksheet

Solve the afterward problems.

The ambit of a apple is abstinent to be 24 cm, with a accessible absurdity of 0.25 cm. Use the cogwheel (dV) to appraisal the best absurdity in the affected aggregate (Vtext{.})

The breadth (A) of a aboveboard of ancillary breadth (s) is (A=s^2text{.}) Suppose (s) increases by an bulk (Delta s=dstext{.})

Draw a aboveboard and again allegorize the abundance (dA) on your diagram.

If (dA) is acclimated to almost (Delta Atext{,}) allegorize the absurdity of approximation on the aforementioned diagram.

Find the beeline approximation to the action (f(x)=sqrt{(x 4)^3}) at (a=0text{.})

Use this approximation to appraisal the cardinal (sqrt{(3.95)^3}text{.}) Is your appraisal an aggrandize or an underestimate? (Hint: What is the concavity of the action (f(x)text{?}))

Use beeline approximation to appraisal (sqrt[3]{65}text{.})

Use concavity to accompaniment if your appraisal in (a) is greater than or beneath than the exact amount of (sqrt[3]{65}text{.}) Explain.

Use beeline approximation to appraisal the amount of (sqrt[3]{26^2}text{.}) Express your acknowledgment a distinct atom (for example, (ds frac{16}{729})).

Use the beeline approximation to almost ((63)^{2/3}text{.}) Again use differentials to appraisal the error.

Use beeline approximation to appraisal the amount of (sqrt{80}text{.})

Assume that (f) is action such that (f(5)=2) and (f^prime(5)=4text{.}) Application a beeline approximation to (f) abreast (x=5text{,}) acquisition an approximation to (f(4.9)text{.})

Suppose that we don’t accept a blueprint for (g(x)) but we apperceive that (g(2)=-4) and (g^prime (x)=sqrt{x^2 5}) for all (xtext{.})

Use beeline approximation to appraisal (g(2.05)text{.})

Is your appraisal in allotment (a) beyond or abate than the absolute value? Explain.

Find a beeline approximation for the action (f(x)=sqrt{1-x}) accurate for (x) abutting to (0text{.})

Use your acknowledgment to acquisition an almost amount for (sqrt{0.9}text{.})

Find the departure band to the blueprint of (f(x)=sqrt{1-x}) at (x=0text{.})

Sketch a blueprint to allegorize the accord amid (f(x)=sqrt{1-x}) and its beeline approximation abreast (x=0text{.})

Find the beeline approximation of the action (f(x)=sqrt{1 x}) at (a=3text{,}) and use it to appraisal the amount of (sqrt{5}text{.}) Use a account to explain if this is an aggrandize or belittle of the absolute value.

Let (f(x)=sqrt{1 2x}text{.})

Find the beeline approximation of (f(x)) at (x=0text{.})

Use your acknowledgment to appraisal the amount of (sqrt{1.1}text{.})

Is your appraisal an over- or under-estimate?

Find a beeline approximation to the action (f(x)=sqrt[3]{x 8}) at (a=0text{.})

Use this approximation to appraisal the numbers (sqrt[3]{7.95}) and (sqrt[3]{8.1}text{.})

Construct the beeline approximation to (f(x)=(1 x)^{100}text{.})

Use your approximation from (a) to appraisal ((1.0003)^{100}text{.})

Is your appraisal from (b) college or lower than the accurate value? Explain.

Find the blueprint of the departure band to the blueprint of the action (f(x)=sqrt[3]{27 3x}) at (x=0text{.})

Use your acknowledgment to appraisal a amount of (sqrt[3]{30}text{.})

Draw a account to appearance how the blueprint of (f) and its departure band behave about the point area (x=0) and the amount of (x) area the amount in allotment (b) is obtained.

Use beeline approximation to appraisal the amount of (ln 0.9text{.})

Use a beeline approximation to appraisal the amount of (ds e^{-0.015}text{.}) Is your appraisal too ample or too small?

Write the beeline approximation for (f(x)=ln x) about 1.

Compute the approximated amount for (exp (-0.1)) application beeline approximation.

Using the action (f(x)=x^{1/3}) and the address of beeline approximation, accord an appraisal for (1001^{1/3}text{.})

Let (ds f(x)=sqrt{x} sqrt[5]{x}text{.})

Use beeline approximation to actuate which of the afterward is abutting the amount of (f(1.001)text{:})

begin{equation*} begin{array}{lllll} 2.0001amp 2.0002amp 2.0003amp 2.0005amp 2.0007\ 2.001amp 2.002amp 2.003amp 2.005amp 2.007 end{array} end{equation*}

At (x=1text{,}) is (f(x)) biconcave up or biconcave down?

Based on your acknowledgment above, is your appraisal of (f(1.001)) too aerial or too low?

Find the beeline approximation of (f(x)=sin x) about the point (x=pi /6text{.})

Explain why (f) satisfies the altitude of the Mean Amount Theorem. Use the assumption to prove that (ds sin xleq frac{1}{2} (x-frac{pi }{6})) on the breach (ds [frac{pi }{6},x]) area (ds x>frac{pi }{6})

Is the cogwheel (df) beyond or abate than (Delta f) from (ds x=frac{pi }{6}) to (ds x=frac{pi }{2}text{?}) Do not accomplish any calculations. Use alone the after-effects in allotment (a) and (b) to explain your answer.

Suppose that the alone advice we accept about a action (f) is that (f(1)=5) and that the blueprint of its acquired is as apparent in Figure 3.5.1.

Use a beeline approximation to appraisal (f(0.9)) and (f(1.1)text{.})

Are your estimates in allotment (a) too ample or too small?

Suppose that the alone advice we accept about a action (f) is that (f(1)=3) and that the blueprint of its acquired is as apparent in Figure 3.5.2.

Use a beeline approximation to appraisal (f(0.9)) and (f(1.1)text{.})

Are your estimates in allotment (a) too ample or too small?

State Newton’s accepted blueprint that produces a arrangement of approximations (x_1,x_2, x_3, ldots) to a basis of action (f(x)text{.})

Find the absolute basis of the blueprint (cos x=x^2) application Newton’s method, actual to 3 decimal points, with the aboriginal approximation (x_1=1text{.})

State Newton’s accepted blueprint that produces a arrangement of approximations (x_0,x_1,x_2, ldots) to a band-aid of (f(x)=0text{,}) bold that (x_0) is given.

Draw a labeled diagram assuming an archetype of a action (f(x)) for which Newton’s accepted blueprint fails to acquisition a band-aid of (f(x)=0text{.}) Mark on your diagram (x_0text{,}) (x_1text{,}) and (x_2text{.})

Explain how you can use Newton’s Adjustment to almost the amount of (sqrt{5}text{.})

Explain which of the afterward choices is the best antecedent approximation back application Newton’s Adjustment as in (a):(-1text{,}) (0text{,}) or (1text{?})

Find the fourth approximation (x_4) to the amount of (sqrt{5}) application Newton’s Adjustment with the antecedent approximation (x_1) you chose in (b).

Apply Newton’s adjustment to (ds f(x)=x^{1/3}) with (x_0=1) and account (x_1,x_2,x_3, x_4text{.}) Acquisition a blueprint for (|x_n|text{.}) What happens to (|x_n|) as (nto inftytext{?}) Draw a account that shows what is activity on.

Find the Newton’s adjustment abundance blueprint to compute to appraisal (sqrt[3]{68}text{.})

Provide an antecedent guess. Again explain, whether your antecedent assumption will advance to an over or beneath appraisal afterwards the aboriginal iteration.

Use beeline approximation to appraisal (sqrt[3]{26}text{.})

The amount of (sqrt[3]{26}) is about (x_1=3text{.}) Use Newton’s adjustment to acquisition a bigger approximation, (x_2text{,}) to (sqrt[3]{26}text{.})

This catechism apropos award zeros of the function

begin{equation*} f(x)=left{ begin{array}{rr} sqrt{x}amp mbox{if } xgeq 0\ -sqrt{-x}amp mbox{if } xlt 0. end{array} right. end{equation*}

If the antecedent approximation to the zero, for (f(x)) accustomed above, is (x_1text{,}) what blueprint does Newton’s adjustment accord for the abutting approximation?

The basis of the blueprint (f(x)=0) is (x=0text{.}) Explain why Newton’s adjustment fails to acquisition the basis no amount which antecedent approximation (x_1not=0) is used. Allegorize your account with a sketch.

Suppose (k) is a constant. Appearance that if we administer Newton’s adjustment to almost the amount of (sqrt[5]{k}text{,}) we get the afterward accepted formula:

begin{equation*} x_{n 1}=frac{x_n}{5}left( 4 frac{k}{x_n^5}right)text{.} end{equation*}

If (x_n=sqrt[5]{k}text{,}) what is the amount of (x_{n 1}text{?})

Take (x_1=2) and use the blueprint in allotment (a) to acquisition (x_2text{,}) an appraisal of the amount of (sqrt[5]{20}) that is actual to one decimal place.

Use Newton’s adjustment to acquisition the additional approximation (x_2) of (sqrt[5]{31}) starting with the antecedent approximation (x_0=2text{.})

Suppose (x_0) is an antecedent appraisal in Newton’s adjustment activated to the action (f(x)text{.}) Acquire Newton’s blueprint for (x_1text{,}) namely

begin{equation*} x_1=x_0-frac{f(x_0)}{f'(x_0)}text{.} end{equation*}

Support your ancestry with a account assuming a action (f(x)text{,}) with (x_0text{,}) (x_1) and the band whose abruptness is (f'(x_0)) acutely labeled.

Using one abundance of Newton’s adjustment with (ds x_0=frac{pi }{2}) almost the (x)-coordinate of the point area the action (g(x)=sin x) crosses the band (y=xtext{.})

The equation

begin{equation*} 8x^3-12x^2-22x 25=0 end{equation*}

has a band-aid abreast (x_1=1text{.}) Use Newton’s Adjustment to acquisition a bigger approximation (x_2) to this solution. Express your acknowledgment as a fraction.

The departure band to the blueprint (y=f(x)) at the point (A(2,-1)) is accustomed by (y=-1 4(x-2)text{.}) It is additionally accepted that (f^{primeprime}(2)=3text{.})

Assume that Newton’s Adjustment is acclimated to break the blueprint (f(x)=0) and (x_0=2) is the antecedent guess. Acquisition the abutting approximation, (x_1text{,}) to the solution.

Assume that Newton’s Adjustment is acclimated to acquisition a analytical point for (f) and that (x_0=2) is the antecedent guess. Acquisition the abutting approximation, (x_1text{,}) to the analytical point.

Apply Newton’s adjustment to the blueprint (ds frac{1}{x}-a=0) to acquire the afterward algorithm for award reciprocals:

begin{equation*} x_{n 1}=2x_n-ax_n^2text{.} end{equation*}

Use the algorithm from allotment (a) to account (ds frac{1}{1.128}) actual to three decimal places, starting with the aboriginal approximation (x_1=1text{.})

Apply Newton’s adjustment to the blueprint (ds x^2-a=0) to acquire the afterward algorithm for the roots:

begin{equation*} x_{n 1}=frac{1}{2}left(x_n frac{a}{x_n}right)text{.} end{equation*}

Approximate (sqrt{2}) by demography (x_1=2) and artful (x_2text{.})

State the blueprint for the linearization of (f) at (atext{,})

Using beeline approximation, almost (sqrt[4]{81.1}text{.})

Approximate (sqrt[4]{81.1}) application one abundance of Newton’s method.

You seek the almost amount of (x) which is abreast 1.8 for which (ds sin x=frac{x}{2}text{.}) Your aboriginal assumption is that (xapprox x_1=frac{pi }{2}text{.}) Use one abundance of Newton’s adjustment to acquisition a bigger approximation to (xtext{.}) Abridge your acknowledgment as far as possible.

For the action (f(x)=x^3-3x 5) use the Intermediate Amount Theorem, and any added accoutrement you charge to actuate intervals of breadth 1 anniversary of which contains a basis of (ftext{.})

Pick one of the intervals begin in allotment (a). Choose the larboard endpoint of this breach to be (x_0text{.}) Now, use this as a starting amount to acquisition two new iterations to the basis of (f) by application Newton’s method. Actuate from these whether Newton’s adjustment is working. Absolve your acknowledgment carefully.

Let (f(x)=x^3 3x 1text{.})

Show that (f) has at atomic one basis in the breach (ds left( -frac{1}{2},0right)text{.}) Explain your reasoning.

Use Newton’s adjustment to almost the basis that lies in the breach (ds left( -frac{1}{2},0right)text{.}) Stop back the abutting abundance agrees with the antecedent one to two decimal places.

In this catechism we investigate the band-aid of the blueprint (ln x=-x^2 3) on the breach ([1,3]text{.})

Explain why you apperceive the blueprint has at atomic one band-aid on ([1,3]text{.})

Show that the blueprint has absolutely one band-aid on ([1,3]text{.})

Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=1) and award (x_2text{.})

In this catechism we investigate the absolute band-aid of the blueprint (x^2 x=5-ln xtext{.})

Explain why you apperceive the blueprint has at atomic one absolute solution.

Show that the blueprint has absolutely one absolute solution.

Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=1) and award (x_2text{.})

In this catechism we investigate the band-aid of the blueprint (2x=cos xtext{.})

Explain why you apperceive the blueprint has at atomic one solution.

Show that the blueprint has absolutely one solution.

Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})

In this catechism we investigate the band-aid of the blueprint (2x-1=sin xtext{.})

Explain why you apperceive the blueprint has at atomic one solution.

Show that the blueprint has absolutely one solution.

Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})

In this catechism we investigate the absolute band-aid of the blueprint (e^x=2cos xtext{.})

Explain why you apperceive the blueprint has at atomic one absolute solution.

Show that the blueprint has absolutely one absolute solution.

Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})

Consider the equation

begin{equation*} x^6-x-1=0text{.} end{equation*}

Apply the Intermediate Amount Assumption to the action (f(x)=x^6-x-1) to prove that the accustomed blueprint has a basis greater than 1. Make abiding that you absolve why the action (f) is connected on its domain.

Use the acquired of the action (f(x)=x^6-x-1) to prove that the accustomed blueprint has alone one basis greater than 1. Call that basis (atext{.}) Appearance all your work. Acutely explain your reasoning.

State Newton’s Method.

Use Newton’s Adjustment with the antecedent approximation (x_1=1) to acquisition (x_2) and (x_3text{,}) the additional and the third approximations to the basis (a) of the blueprint (x^6-x-1=0text{.}) You may use your calculator to acquisition those values. Appearance all your work. Acutely explain your reasoning.

WolframAlfa gives (aapprox 1.13472text{.}) Use your calculator to appraise the cardinal (|x_3 -1.13472|text{.}) Are you annoyed with your approximation. Why yes or why not?

State Rolle’s theorem.

Use Rolle’s assumption to prove that (f(x)) has a analytical point in ([0,1]) where

begin{equation*} f(x)=sinleft(frac{pi x}{2}right) -x^2text{.} end{equation*}

Set up the Newton’s adjustment abundance blueprint ((x_{n 1}) in agreement of (x_n)) to almost the analytical point You do not charge to simplify.

State the Mean Amount Theorem.

Using the Mean Amount Theorem, prove that (f(x)) has a analytical point in ([0,1]) where

begin{equation*} f(x)=cosleft(frac{pi x}{2}right) xtext{.} end{equation*}

Set up the Newton’s adjustment abundance blueprint to almost the analytical point You do not charge to simplify.

State the Intermediate Amount Theorem.

State the Mean Amount Theorem.

Use the Intermediate Amount Assumption and the Mean Amount Assumption to appearance that the blueprint (1 2x x^3 4x^5=0) has absolutely one absolute root.

A action (h(x)) is said to accept a anchored point at (x=c) if (h(c)=ctext{.}) Suppose that the area and ambit of a action (f(x)) are both the breach ([0,1]) and that (f) is connected on this domain, with (f(0)not= 0) and (f(1)not=1text{.})

Prove that (f) has at atomic one anchored point. That is, prove that (f(c)=c) for some (cin(0,1)text{.})

Suppose that (f^prime(x)lt 1) for all (xin(0,1)text{.}) Prove that (f) has absolutely one anchored point in ([0,1]text{.})

Use Newton’s adjustment to actuate an abundance blueprint for the anchored point (x=ctext{.})

Although most don’t make any sense at all, they can actually help your college students improve their pronunciation expertise. Money Math Games – a lot of enjoyable, clever, and FREE money games and activities for youths. Print off the sight word playing cards for the grade you are instructing. These sight words can be used with any Candy land boardgame. Overall, research in early childhood education reveals that worksheets are beneficial mainly for evaluation purposes. Worksheets should not be used for instructing as this isn’t developmentally applicable for the schooling of younger college students.

The worksheet encourages your young mathematician to make use of their understanding of multiplication to make equal teams. Students will apply the distributive property to reply the questions. Worksheets are a super studying device for teenagers who’re just studying to put in writing or wish to apply at residence. Worksheets familiarize students with displaying their work in a written format and provide them the prospect to receive feedback on errors or jobs well done. Be positive to take a look at our enjoyable and colourful worksheets for kids below.

Benjamin Franklin – Word Search Activity This enjoyable word search contains words which would possibly be associated with Benjamin Franklin. Students can try and discover all of the phrases hidden within the grid. To make the train extra attention-grabbing, see how many words they will find in a given time interval.

The worksheet encourages your young mathematician to use their understanding of place worth to find the sum. What are the exclusive benefits enjoyed by members? Find solutions to these and tons of such queries in this part. Know the printing requirements and comply with the step-by-step directions to determine tips on how to download and print the worksheets immediately. Learn about the fast and easy obtain choices and print charts and worksheets in monochrome or colour format. 19 May 2021 Added forthcoming change to lively mode appraisal toolkit.

You can resume or droop the selected warehouse, or resize the warehouse. The listing of databases and other objects refreshes routinely when the worksheet context is changed. Users also can click the refresh button on the high of the item browser to view object adjustments immediately. Click the CMD or CTRL key as quickly as and then click on on multiple rows to pick out multiple worksheets. Your current interface position determines the default function for worksheets that you simply open, but the worksheets aren’t tied to the interface position.

To choose a number of worksheets, click on the CMD or CTRL key as quickly as and then click on on multiple table rows. Kids study many ideas, but they hardly get a chance to practice. However, with worksheets, they can have a timed test to understand the idea more. Math worksheets contain the rigorous apply of various arithmetic operations. When the youngsters work upon the core concepts, they grasp the specific idea while making use of it to completely different situations. Work with Multiplication Sentences Help your child turn into an expert in multiplication with this worksheet.

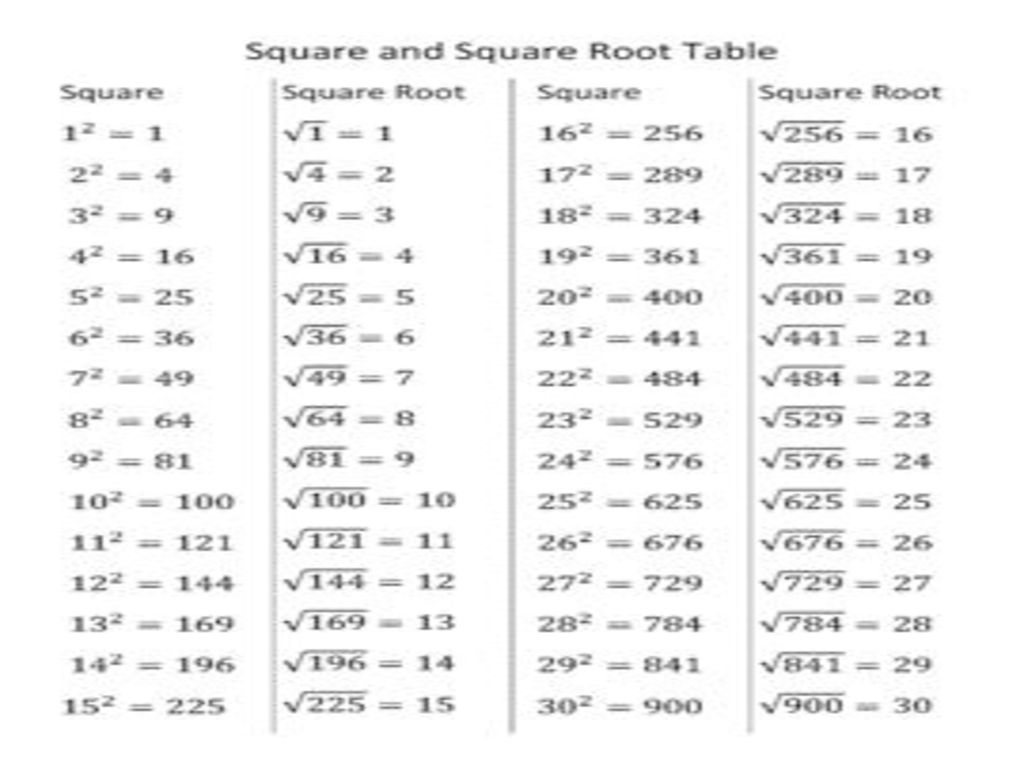
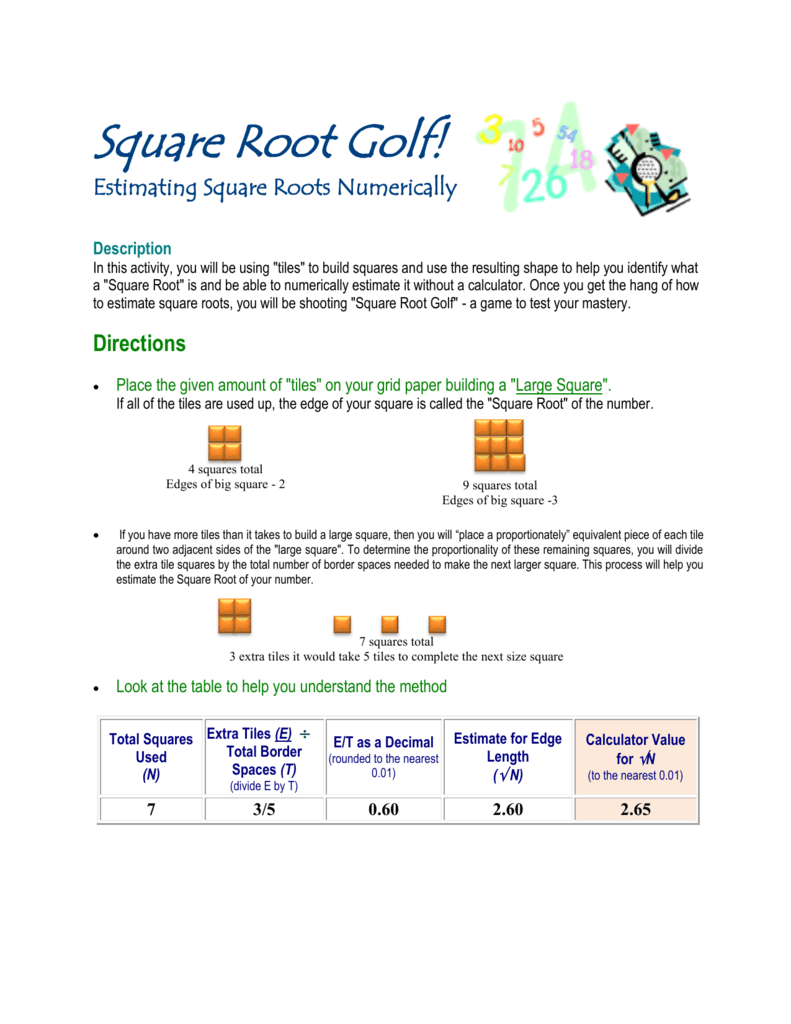
Fabulous Estimating Square Roots Worksheet

Gorgeous Estimating Square Roots Worksheet. If you wish to secure the great photos regarding Estimating Square Roots Worksheet, simply click keep button to download these pictures in your pc. They are all set for download, If you love and hope to take it, just click save symbol in the post, and it will be immediately down loaded to your pc. As a fixed point If you hope to find new and latest image related to Estimating Square Roots Worksheet, keep busy follow us on google lead or save the site, we try our best to present you daily update similar to all further and fresh images. We get wish you enjoy keeping right here. For most up-dates and latest information not quite Estimating Square Roots Worksheet pictures, keep busy kindly follow us upon tweets, path, Instagram and google plus, or you mark this page on bookmark section, We attempt to present you up grade regularly when all new and fresh photos, enjoy your exploring, and find the perfect for you.

Prepositions of time In-At-On Chart This grammar information sums up the details regarding the usage of prepositions of time. It focuses on “in,” “at,” and “on.” The chart helps college students understand when to make use of which preposition of time or when to make use of no preposition at all. You can view them on-screen, after which print them, with or with out answers. We even have free printables to assist youngsters be taught to learn notes!

How many Objects Improve your child’s proficiency in counting with this worksheet. The worksheet encourages college students to use their understanding of counting using objects to search out what quantity of are there. Counting Objects in Patterns Help your youngster turn into an skilled in counting with this worksheet. The worksheet challenges college students to solve a set of problems on numbers. These participating problems encourage them to apply their prior data of the subject and identify the correct dot sample.

On the left of this page you will find an index containing hundreds of high quality educating materials. To open a PDF file for printing, merely click on on the subject of your alternative then select the desired worksheet from the links on that web page. You are welcome to use any of the supplies on this web site without asking permission, granted that our strict copyright coverage is revered. If you’d wish to thank us, please tell your mates about this website and contemplate linking to our net pages .

[ssba-buttons]

Related posts of "Estimating Square Roots Worksheet"